
出品:新浪科技《科学大家》、墨子沙龙
演讲者:David·Wineland 物理学家,科罗拉多大学物理系教授,2012年诺贝尔物理学奖的获得者
大家都知道计算机和iPad如何工作的,那么量子力学对计算机又有什么影响呢?这跟量子系统中可以实现的一些奇异的性质有关,其中一种性质就是叠加态。

什么是叠加态呢?在上面这个图片中,大家看到线段画成的立方体,有时候是左边正方形在前面,有时候你又会看到右边正方形在最前面,所以你看到哪个面有某种不确定性。如果你看一会儿右上角的正方形,也许就可以看到一个图片。这个图片同时有两个属性,这非常像我们在量子力学中所说的叠加态。比如量子比特就可以同时有两种性质,如果我们有一个两个态的系统,就像上图看起来这样:当你试图从一个方向到另一个方向看时就非常类似量子测量,也就是在右手边的角上你可以同时看到两面,但是当你倾向看一个或者另一个图片的时候就非常像(测量)投影。
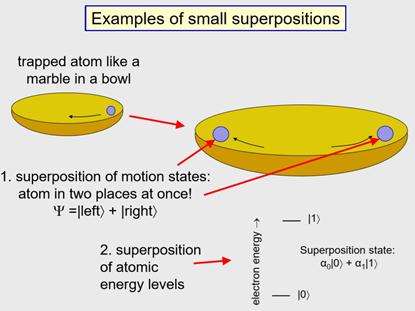
还有一些小系统叠加态的例子:比如量子比特,是处于势阱中的原子,你可以把它想象成碗里的弹珠,弹珠可以在碗里来回地滚动,我们通过“碗里”的原子就可以实现一种叠加态。
这种条件下,有时候原子同时处在“碗”的左边和右边,而这在日常经验中讲不通,但是在量子系统中就可以实现。这就是叠加态的一个例子,即有时候原子可以同时处在左边和右边的叠加态。对于利用叠加态来做量子计算机,我们感兴趣的是利用原子的电子内态作为量子比特,比如可以把最低能态标记为|0>,把相邻的较高能态标记为|1>,利用这些不同的能态就可以在量子系统中组成普通的量子比特。但是我们也可以用它们的叠加态,也就是同时处在 |0>和|1>态。

关于量子计算的内容就不在此赘述了,但我想让大家理解它为什么有意思。经典计算机里一个比特可以是0或1,但是量子比特中,它可以同时是0和1,所以量子计算机有意思的一方面是量子寄存器是如何按比例增加的。比如3比特的内存寄存器,通常的经典计算机中可以存储一个3比特的二进制数,比如101,但是如果是叠加态,量子寄存器就可以同时存储从000,001一直到111,也就是所有的8中可能存的数。所以我希望你们能从中学到的是量子比特的这种大量并行内存,可以同时存储所有这些数。
所以有意思的就是,从我刚才举例的3比特量子寄存器中,可以同时存储所有8个3比特二进制数,8等于2的3次方,也就是每个比特的态数目的幂,幂次是比特数目。有意思的是,我们可以假设有300个量子比特,那就可以同时存储2的300次方个数,也就是大概10的90次方个数,这比宇宙中所有基本粒子的数目还要多。
某种意义上讲,300个量子比特的内存,可以存储的容量比所有宇宙中物质制作的经典内存还要多,听起来就很有趣。这些系数的值一般不同,它们是用来表示处在|000>、|111>之类·的态上的概率,用来区别这些概率。另外当我们对量子比特做一次操作时,只要翻转第一个比特,通常这样会马上改变所有这些量子寄存器前面的系数。这样的写法是量子力学里面写波函数的标准写法。量子计算机非常优秀,这种问题不存在的。
但是还得用量子力学来实现一些前提,首先考虑到量子力学时,你会想到可以制成这些量子叠加态,但是当你真正继续测量量子系统时,这里的量子叠加态就会坍缩到一个态上去。换句话说,这个存储8个二进制数的寄存器,当我们测量它的时候,无论有多少个比特,都会坍缩成为其中的一个二进制数,所以当你测量一个300量子比特的计算机,它会坍缩成“一个”300比特的二进制数,这听起来是严重的限制。
1995年左右,计算机理论学家Peter Shor提出了一个计算机算法,说假如可以制成量子计算机就可以有效的进行大数分解。如果一个非常大的数,可以表示成两个更小的数的乘积,我们可以找到这两个小的因子,对于非常大的数,比如300位的十进制数,这是非常困难的问题。但是Peter Shor得到了大数分解的非常有效的方法。我要说,你们很多人应该知道,这有意思的理由是如果可以分解大数,基本上几乎所有提供隐私的加密。
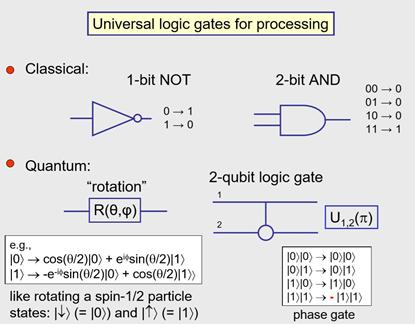
比如购物时使用信用卡,你获得的安全和隐私是因为大数难以分解,如果可以制成这样一个机器,毫无疑问,它不仅可以用在信用卡上,还对国家机密有用。相对于经典计算机,量子计算机又是什么样的呢,结果发现,可能制作一台经典计算机并不是最有效的。基本上的做法只需将两个门结合起来用就可以做任何一种计算,一个是比特翻转门,另一个是一种非平凡的2比特逻辑门,这里这个门是2比特的“与门”。
量子比特中也类似,这里(单比特操作)不只是简单的比特翻转,而是(相位)“旋转”,基本想法是用向量表示量子比特,(经典计算中)向量方向可以朝上或朝下。但是量子世界中,向量可以朝向任何方向。此外,我们还想让这个比特有比比特翻转更通用的性质,比如这里这个2比特l量子逻辑门,这个相位门的两边的列表中,看起来除了在特定的位置提取出一个负号什么都没做。
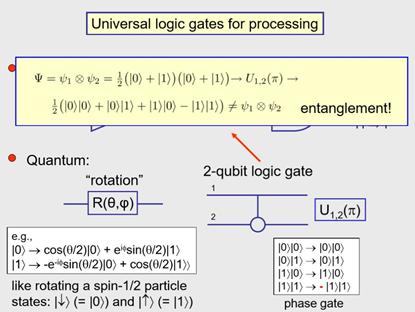
这一过程的有趣之处在于,如果有两个量子比特都处于|0>和|1>的叠加态,然后做这个相位门操作,得到的波函数表示的是,这两个在量子比特的初态时是相互独立的,但是通过这个相位门发现,这两个量子比特不能再写成性质相互独立的波函数了,我们把这叫做纠缠,(纠缠态下)如果测量一个比特,会影响另外一个比特的值。

上图是Peter Shor发明Shor算法时的照片,在他之前还有其他理论学家提出过想法,但是Peter Shor的算法影响到了安全,这个方向火了起来,政府开始感兴趣,并且非常想资助这类研究,直到今天这种兴趣还持续增长。在中国,大家花了很大的兴趣来制造量子计算机和相关的器件,所以这类热度一直在增长。
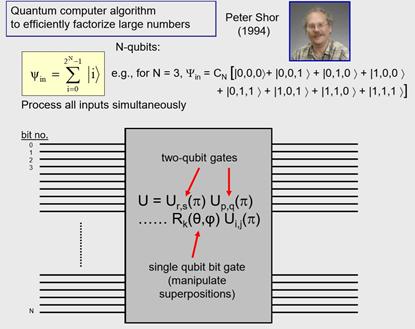
实际上,这不算是个特别神秘的算法,跟做经典编程的方法区别并不很大。这个算法工作的一个非常简单的解释是加入要分解大数,插入一个叠加态,这个态包含直到需要分解的大数的所有数,以及用来做计算需要的一些额外的比特数,但是基本上跟经典计算机里的线路编程没有很大的不同,这个算法的思路就是输入相当于所有这些可能数值的叠加态,然后运用一系列的2比特逻辑门和单比特的旋转操作,改变向量的方向,这样就可以简单地解释算法怎么运行的,一定程度上来讲并不是很神秘。
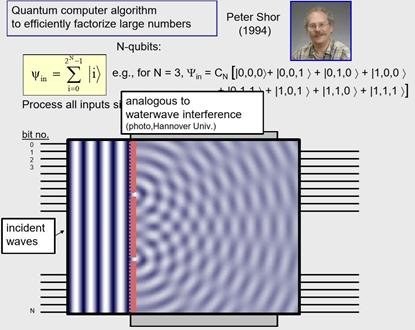
很多人刚上物理课的时候应该就看过这个图了,有水波实验的甚至可能做过实验了。这里这个波动的示意图的内涵是如果一个波冲向这个障碍物,障碍物上有一系列小的开口,就会有一些波传过。事实上这些波通过障碍物并干涉,就会得到相长干涉和相消干涉,量子系统中我们的做法其实(类似),可以把量子系统一定程度上看作复杂得多的干涉实验,但是本质上同样都是把量子比特相互干涉。
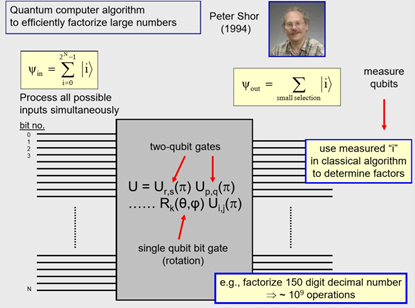
其中有很多的细节,按照Peter Shor的想法做算法操作,然后最后得到量子寄存器,在他的算法中,理想状况下测量概率的时候,仍然有一些态。但结果是,他在算法中证明,这些态中的任意一个都可以用经典数论算法给出因子。
我们面临的困难和目前的处境是什么呢?比如分解一个150位的十进制数,需要大约10的9次方次操作完成分解。而我们目前的实验仍然非常简单,目前,我们可以做几百次操作不出现错误,但是超过几百次,就很难做到10的9次方次操作了,所有还有很长的路要走。还有另外一个完整的研究方向,Peter Shor参与了部分开拓,他证明量子力学中其实可以进行纠错,但那是大学里一整个的子分支方向,这里不过多介绍。
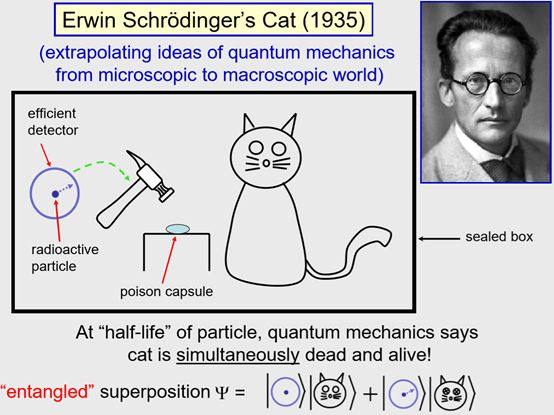
薛定谔是量子力学的发明者之一,他的版本被称作波动力学。根据薛定谔的理论,会得到这样一个结果,假设(理论)一切完美,那么原则上可以制作一个非常大的叠加态,而薛定谔认为如果可以这样的话,量子力学就有些不对的地方,他为了表示自己对理论的担忧和不满提出一个理论,原则上可以写出这样一种状态的量子力学方程。
然后他假设,有一个跟外界干涉隔离的箱子被封起来,箱子里面这个地方有一个放射性粒子,还有一只猫。他虚构的例子是,如果放射性粒子衰变存在这样一个机械装备可以释放毒剂杀死猫,原则上我们可以写下量子力学方程来描述它。真的写起来也很麻烦,这是薛定谔写的方程,他说经过放射性粒子的半衰期后,粒子有50%的概率会衰变。量子力学告诉我们的是,猫处在活或者死的状态,这是一种叠加态,同时处在放射性粒子没有衰变且猫活,和粒子衰变且猫死的叠加态。
我刚才说过,他虚构这个例子的原因是,原则上量子力学可以延伸到大尺度,或者说我们生活的宏观世界,他整个职业生涯都非常关心这件事。

而实际上,直到50年代,他发明波动力学很多年后,关于系统如何延伸的想法,来自于像爱因斯坦、薛定谔和海森堡这样的人坐下来思考量子力学的结果,薛定谔的猫是其中一个例子,反正薛定谔在他的整个职业生涯都为这个问题所困。他说,“我们从没用单个电子、原子或者小分子做实验”。他们这就是这样,刚开始的时候思考小实验,在“思想实验”中,德语叫“Gedanken Experiment”,“我们有时候假设这样做,“但是这样总是不可避免一些荒谬的结果”,也就是这只猫。
现在这些思想实验对我们物理学家来说就是我们的世界,我们做不出像猫一样大的物件,但是实际上可以实现所有这些基本的想法,里面没有魔法,结果显示我们需要的是对系统的精密控制。。。。。需要跟外界环境隔离开。我觉得有意思的这两个例子就是原子钟和量子计算机,我这次只讲一下量子计算机,其实全世界还有很多人都在思考这个问题,有几百个小组在做这样的实验研究。
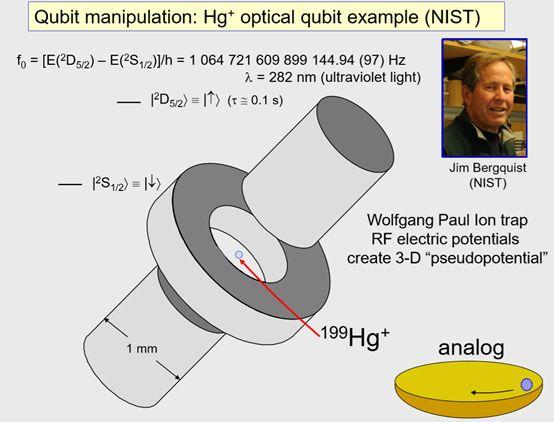
如何对量子比特进行操控?上图是我在NIST(国家标准与技术研究所)做实验的一个同事,这个实验的量子比特是基于两个能级差为光频的原子能级,对应的波长在紫外波段,这是写原子物理的记号,能级低的态叫做“自旋向下”态,能级较高的态是箭头指向上的态。反正这样的实验中,最简单的版本就是离子阱里面的单个离子,这是以发明者Wolfgang Paul命名的射频势阱,保罗阱产生一个跟弹球在碗里类似的三维势阱,可以把这个设备想象成这里表示的一样。
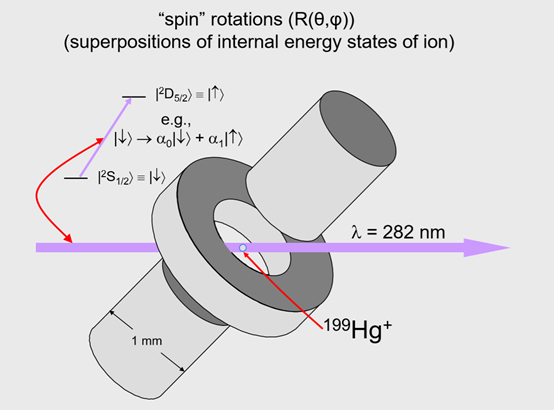
那么我们如何制作叠加态呢?我们可以把原子制备在“自旋向下”的态,也就是能量最低的态,然后打一段时间的激光,让激光开一定的时长,然后原子内态就从基态演化成叠加态。
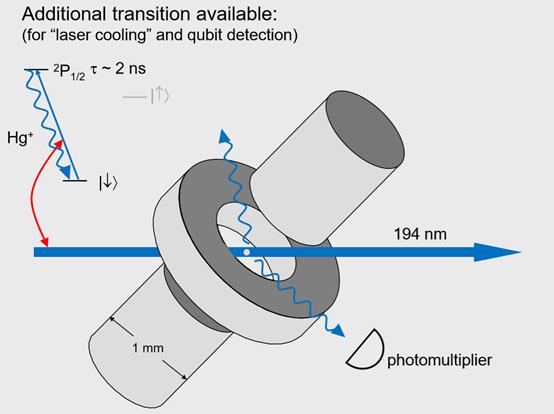
这个实验中原子还有另外一个跃迁可以利用,从基态到这个更高能量的激发态。这一个态可以维持很长时间,虽然只有几十秒。可能大家觉得很短,但是相对于实验中的周期来讲要长的多,所以基本可以认为实验过程中原子一直呆在这个态上。
测量这个态要做两件事,一是利用另外一个跃迁的光打在原子上,这个激发态会很快衰变,寿命只有2纳秒,也就是说如果原子在这个激发态上就会很快的衰变,我们就可以从离子散射出相当多的光。
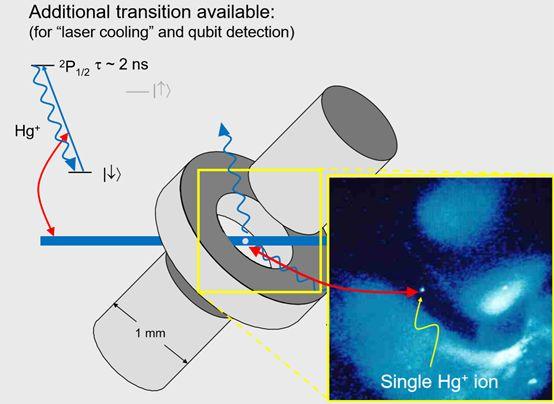
实际上可以对离子拍照,上图是离子阱中单个离子的一张照片。有意思的是这个跃迁的波长也是紫外光,但是也有一些离子,它们会发出可见光,比如钡离子就会散射蓝光,实际上在钡离子实验室,你可以用肉眼加一个小的放大镜就可以看到单个粒子,用一个小放大镜就可以看到单个原子真的是让人非常惊奇,看起来就有点像小星星。
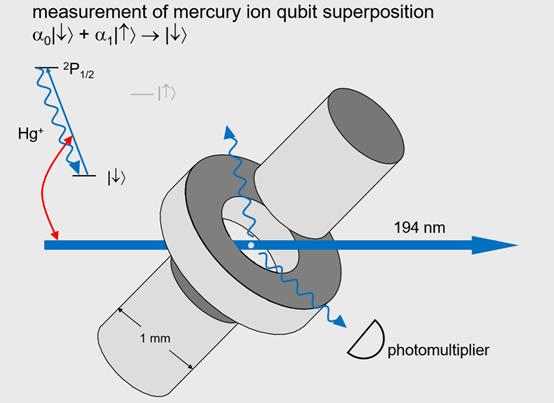
这个跃迁很有意思,它可以用来冷却原子,其中的原理是当原子散射光时,它们感受到光辐射压力,来自被散射光子的动量,这就形成对原子的作用力。我们可以通过实验条件让原子只吸收或者散射传播方向与原子运动方向相反的激光,来让原子慢下来,比如我们可以在实验中,300K的室温条件下,通过激光冷却原子的方法将原子从300K冷却到1毫K,但更多的细节就不过多展开了。
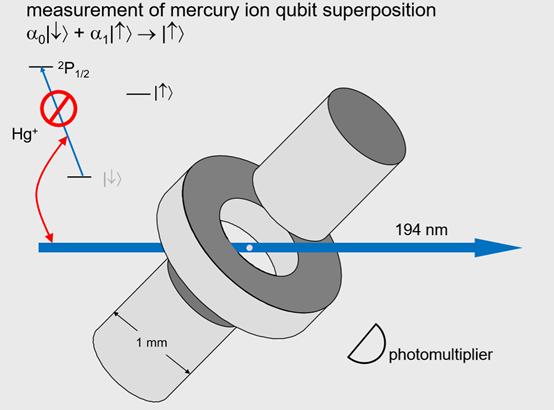
我们也可以用这个跃迁测量原子的态。假设制备了这个叠加态,当我们打开这束激光,进行测量,也就是的“投影”。如果原子被投射到上能级,那么就不会有散射,我们探测不到光。
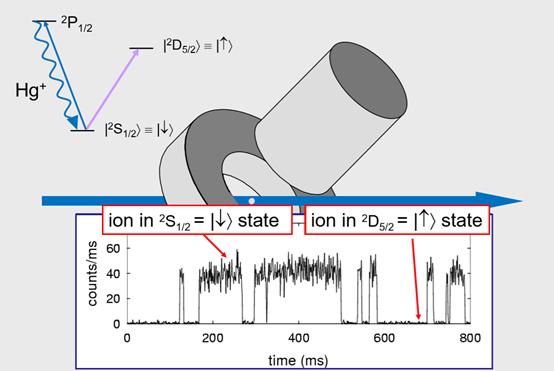
如果原子被投射到这个态,就看不到荧光,如果被投射到这个态上我们就可以看到荧光,这样我们就可以通过荧光、散射的光,用探测器进行探测。如果原子被测量到,也就是投影到,这个低能级态,我们可以看到光,如果被投影到较高能级的态,就看不到光,或者只有很弱的背景散射光。还有一点比较好,我们可以设一个阈值,来区分有没有荧光,这样可以达到100%的探测效率,我们还可以在这个实验条件下做些其他的事情。
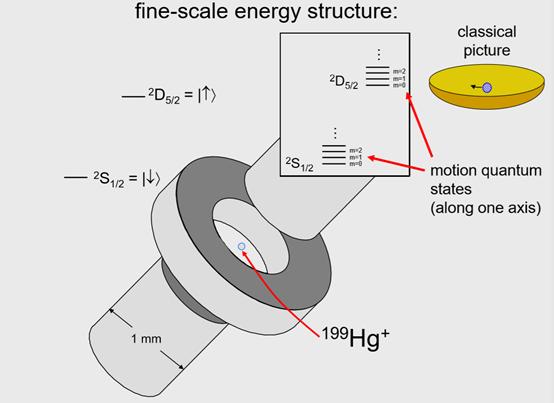
我说过一个经典图像,原子像弹球一样在碗里滚来滚去,但实际上这个原子“弹球”也是一个量子系统。量子力学告诉我们原子“弹球”的能级,其实是离散的能级,像这里表示的一样。这些m给出原子所在的运动态,在刚才讨论的简单的量子计算机中我们需要这些能级,现在们需要的是把这个量子化的谐振子冷却下来,到最低的动能能量态,也就是我们说的运动基态,冷却的方法其实非常简单。
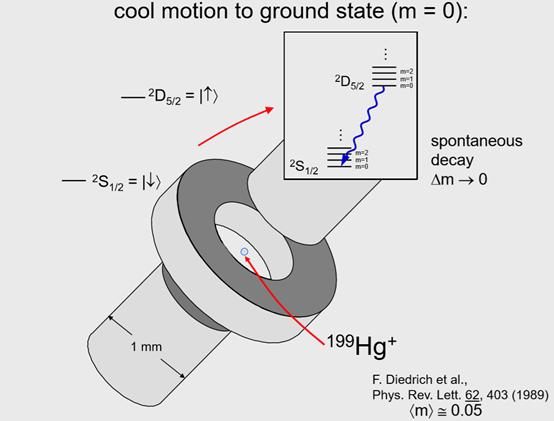
可以用激光驱动原子跃迁,这样激光就会使原子从较低的能态到较高的能态,也就是从“自旋向下”态到“自旋向上”态,驱动原子跃迁时也可以使原子的动能减少一个能级差的能量,结果就是,在实验中我们可以实现这样一种条件。当原子衰变散射光子时,原子可以冷却而动能能级不改变,基本上需要做的就是让激光开一会儿,然后让原子持续激发到较高的能态并减少一个量子数的能级,最终原子就会衰减到基态,这就是制备动能最低能态的方法。

1994年,Artur Ekert从罗拉多的Boulder参加我组织的原子物理会议,他那时候已经知道Peter Shor的算法了,并且告诉了原子物理学家们。当时在听报告的还有两个著名的理论物理学家,Ignacio Cirac和Peter Zoller,他们是非常优秀的理论物理学家,但同时也知道实验是如何进行的,他们迅速地提出一个理论,可能可以实现量子计算机,理论思想是下面这样的:
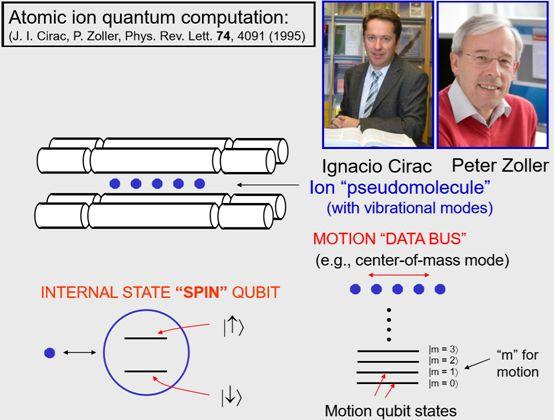
这个势阱跟我们的“碗”模型类似,有一点不同,但仍然是三维的谐振势阱。这个势阱里,我们把水平方向也考虑进来,这里很显然是相较其他两个方向,所以如果把这些带电的电子,也就是离子放进三维的“碗”中,然后用激光冷却下来。
那么他们都想落到碗的底部,在这个方向会有这样一种最小能量点,但另一方面由于原子带电,库伦排斥力会将它们分开排成规则的队列。这很有意思,因为这样我们可以控制聚焦的激光跟不同的离子作用,某种意义上这里这个例子中,就是离子组成的5个量子比特,看起来就是5个原子组成的“分子”,或者一个“赝分子”,跟通常的分子一样,它也有震动模式。
结果证明,他们各自都有不同的频率,因为他们的频率不同所以我们可以隔离出其中一个震动模式(来进行操作)。首先最容易想到的模式就是5个离子在势阱中沿着这个方向,来回滚动位置的模式,所以他们两人提出制作量子计算机的方法就是像我刚才说的那样,首先用激光冷却原子到基态,首先要把所有离子的运动状态制备到基态,然后他们的方案中第二步是,大体来讲,做量子计算的每个离子链上的每个离子都在它们的内态的叠加态上。
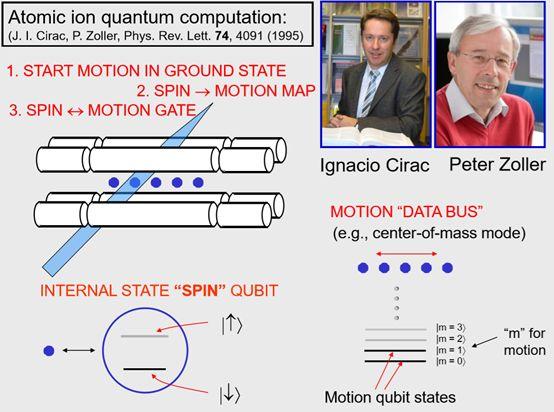
然后他们的想法是,如果可以把离子内态的叠加态通过某种方式映射到运动的第一激发态,那么基本就可以把离子的内态量子比特转化成运动状态的量子比特,而事实上运动的量子态在离子之间是共有的。然后他们提出,如果可以以某种方式对运动状态的量子比特做逻辑门操作,比如这里的第二个离子,那么基本上也就通过这种映射完成了第一个和第二个离子之间的逻辑门操作。
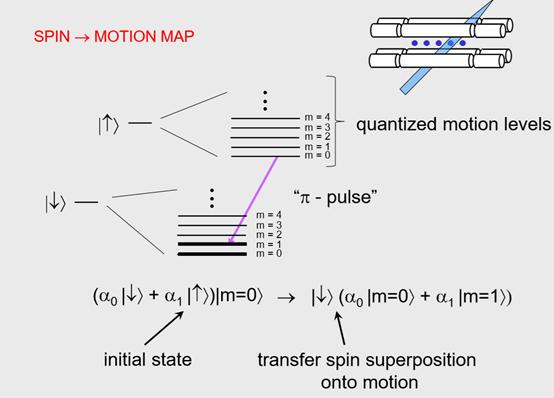
我在NIST(国家标准与技术研究所)时,有过一篇文章阐述这个观点,大家正好都在一起,那时候我的同事Chris Monroe正好也在NIST,文章里的工作完成了逻辑门操作,是对最后这个态的操作,既然我们可以对两个离子做量子逻辑门操作,那么也可以在一串序列中选择离子来做逻辑门操作,这也是量子计算这个方向的关键思想。
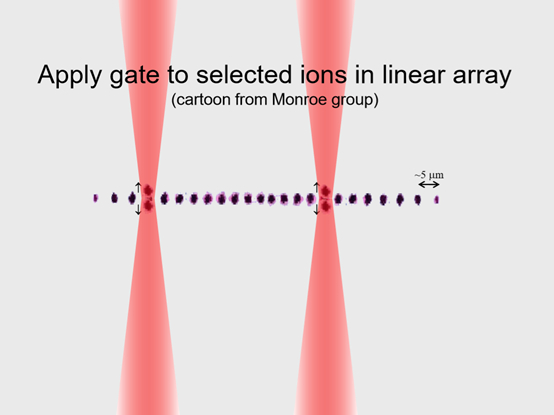
大家想在量子计算机中能够将任意量子比特联系起来,这是一个实验结果,这个结果来自Chris Monroe和我的同事组成的公司,这里他们展示的结果基于11个离子序列的量子比特,可以完成任意离子之间的量子逻辑门操作。
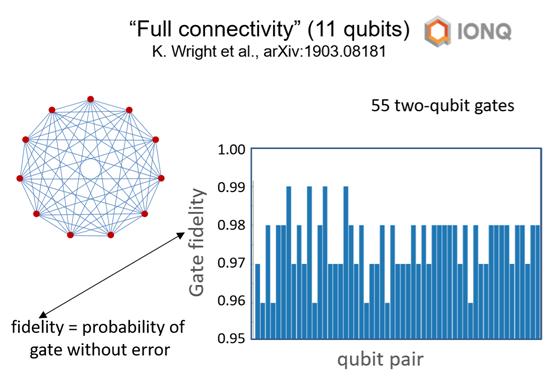
我们不止可以做量子计算,也可以用一个量子系统来模拟另一个量子系统,很多人对这个感兴趣,包括Chris Monroe,我的朋友和同事Rainer Blatt,他来自Innsbruck,Peter Zoller也在那里,还有我在NIST的同事John Bolinger。他们已经可以模拟单原子系统之间的一些复杂的相互作用,那么怎样扩展到更大的数目呢?

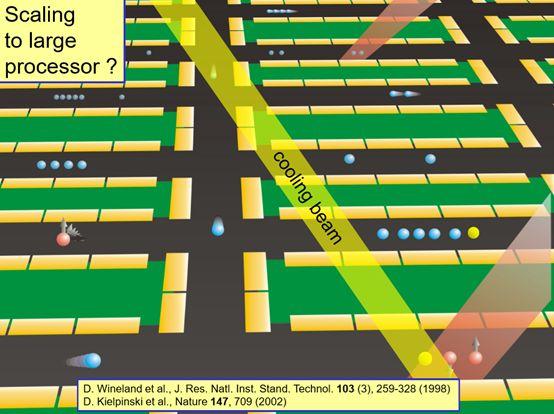
一种方法是,不是在单个三维势阱中完成所有操作,而是这样来做,我们可以做成大批这种单个的小序列。按照需要移动这些离子,比如这里的两个离子做逻辑门,它们在这个大序列中处在不同的位置,然后把它们移动到这个位置来做逻辑门。
这些只是我知道的用离子研究量子计算小组,所以大家可以看到全世界有很多小组,而且还有用其他物理平台进行实验的小组,有些基于超导体,有些基于量子点或者凝聚态系统等,所以全世界有大量的研究组在开展这项研究。

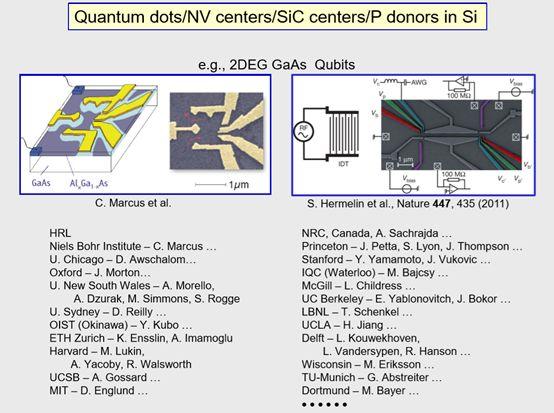
未来是什么样子呢?目前的量子计算操作还有太多的错误,所以我们需要提高逻辑门的准确性,这可能是最重要的事,我们也需要扩展规模的方法,还有我开始就讲过的Peter Shor的大数分解算法,还有量子模拟,我想你们很多人或许对这个更感兴趣,因为量子模拟在帮助人们解决大量物理难题方面可以是非常通用的。结果证明量子世界中我们可以利用特殊的量子态来提高测量灵敏度,大体上我们把这称作计量学,这些是实现的方法。还有有意思的是,你们可能已经听说过,现在有一些商业公司也在做量子计算的研究,所以不只有世界上的这些实验室在做。

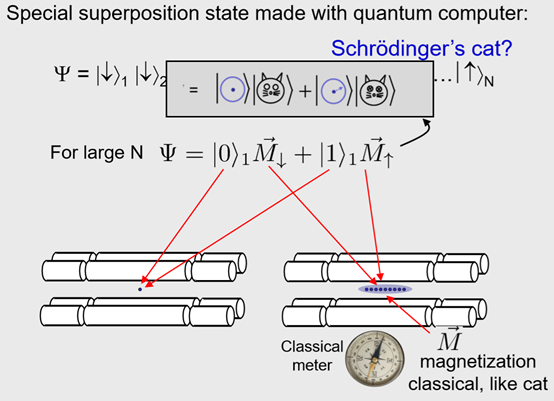
我做一下总结,我谈了一点薛定谔的猫,至少证明现在在较小的尺度,我们可以制作这样一个态,它就是所有量子比特同时较低能级和较高能级的叠加态。实验中的做法是,结果证明量子比特表现得就像小磁铁一样,具有磁矩,大量的量子比特,就会表现的更像一个宏观的磁铁,所以我们可以把这个量子态,比如选择第一个量子比特,把它移动到这个区域,而这个区域里有剩余的量子比特,如果数目足够大的话,这就像是一种宏观的磁化。原则上我们就可以用经典的仪表比如指南针什么的来测量它,所以我们就可以说这就非常像是个薛定谔的猫了。如果用一个微观系统,我们这个例子里就是一个量子比特,而薛定谔的理论中是一个放射性粒子,外加一个特殊的纠缠态,也就是薛定谔的例子中的猫,“死”或“活”对应经典的磁化的指向为上或者指向下。
最后对实验来说最重要的是参与研究的这些人,这是一年前的照片,这是在科罗拉多的Boulder的小组,我现在也还在Boulder有任职,当然真正的工作是一大批博士生、博士后和同事共同完成的。对我来讲参与其中很有意思,但是这些成果的产生离不开所有这些人。
注:本文根据墨子沙龙演讲内容整理而来,有删减,部分图片由演讲者提供。




