近100年来,几乎所有科学家在分析实验数据时,都会用到p值这个工具:只有p小于0.05,才意味着实验结果具有统计显著性,才能在学术期刊上正式发表。但是,统计显著性的概念以及支撑它的p值具有相当大的局限性。而正是这样的缺陷,让整个科学界都处于危机中。
这篇选自《环球科学》11月新刊的文章,为我们讲述了P值危机。

1925 年,英国遗传学家兼统计学家罗纳德·菲舍尔(Ronald Fisher)出版了《研究者的统计方法》(Statistical Methods for Research Workers)一书。这本书的书名在当时看起来并不会“畅销”,但实际上这本书却取得了巨大的成功,而且还使菲舍尔成为现代统计学之父。在这本书中,他着眼于研究人员如何将统计检验理论应用于实际数据,以便基于数据得出他们所发现的结论。当使用某个统计假设来做检验时,该检验能够概述数据与其假设的模型之间的兼容性,并生成一个p值。
菲舍尔建议,作为一个方便的指南,研究人员可以考虑将p值设为0.05。对于这一点,他专门论述道:“在判断某个偏差是否应该被认为是显著的时候,将这一阈值作为判断标准是很方便的。”他还建议,p值低于该阈值的结论是可靠的,因此不要把时间花在大于该阈值的统计结论上。因此,菲舍尔的这一建议诞生了p小于0.05等价于所谓的统计显著性,这成了“显著”的数学定义。
菲舍尔的遗憾
近一个世纪之后,在科学研究的许多领域,p值小于0.05被认为是确定实验数据可靠性的金标准。这个标准支持了大多数已发表的科学结论,违反这一标准的论文很难发表,而且也很难得到学术机构的资助。然而,即使是菲舍尔也明白,统计显著性的概念以及支撑它的p值具有相当大的局限性。
P值经常被曲解,统计的显著性不等于实际的显著性。此外,为了让数据更漂亮,很多研究人员有意无意地将p值向上或向下调整。美国加利福尼亚大学洛杉矶分校的名誉教授、统计学家和流行病学家桑德·格林兰德(Sander Greenland)说:“你可以用统计学方法来证明任何事情。”他是呼吁统计学改革的科学家之一。只依靠达到统计显著性的研究经常会得出不准确的科学结论,这种判断标准可以把真的事情判断为假的,也可以把假的事情判断成真的。在菲舍尔退休,移居澳大利亚后,有人问他,在漫长的职业生涯中他是否有任何遗憾,他明确回答道:“当初不该提出0.05。”

统计学家罗纳德·菲舍尔。图片来源:维基百科
在过去十年里,关于统计重要性的争论以不寻常的强度爆发。援引两篇论文的观点:一篇文章称统计分析的薄弱基础导致了“科学最肮脏的秘密”;另一篇则提到,在检验某些假设时,存在“许多深层次的缺陷”。在争议声中,实验经济学、生物医学研究,特别是心理学被卷入了一场科学实验可重复性的危机之中。在这场危机中,科学家发现相当一部分研究是不可重复的。
一个臭名昭著的例子是“姿态能量”的概念,某篇论文声称,自信的肢体语言不仅会改变你的态度,还会改变你的激素分泌,后来这篇文章还被作者自我否定了。美国哥伦比亚大学的统计学家安德鲁·格尔曼(Andrew Gelman)在他博客写道:“一篇可疑的关于气候经济学影响力的论文,多年之后发表了勘误声明,最终被修正的错误结论几乎与原论文的数据点一样多,这可不是开玩笑!但勘误声明中这些更正都不足以让作者改变结论。” 格尔曼还说道:“嘿,只做理论上的工作就可以了,但不需要用数据分散我们的注意力。”
统计显著性的概念虽然不是引起问题的唯一因素,但很明显,它是引起问题的一个关键要素。在过去的三年里,数以百计的研究人员呼吁统计学改革,他们在著名期刊上发表文章,重新定义统计显著性,或干脆放弃统计显著这个概念。美国统计协会(ASA)在2016年就这一问题发表了一份强有力且不同寻常的声明,主张“进入一个没有p<0.05的世界”。美国统计协会执行董事罗纳德·瓦瑟斯坦(Ronald Wasserstein)这样说:“科学家总是说,我有小于0.05的p值,这很好。但这种粗糙的判断方法,使得科学因此停止了。”

问题是,事态会不会有什么变化。美国南加利福尼亚大学的行为经济学家丹尼尔·本杰明(Daniel Benjamin)表示:“这已经不是新鲜事了。我们需要清醒地认识到,这一次将与以往一样,大家说要变革统计学,最终却不了了之。”很多人在变革统计学的具体措施上有分歧,正如美国经济学家斯蒂芬·齐利亚克(Stephen Ziliak)所写的那样:“令人吃惊的是,还有不少研究者坚持使用统计显著性检验、统计结论解释和统计分析报告这三个例行公事的传统套路。”
可重复性危机
科学的目的是描述自然界中的真实情况。科学家使用统计模型来推断真相,比如确定一种治疗方法是否比另一种更有效。每个统计模型的分析结果,取决于科学家如何收集数据,如何分析数据,以及研究人员如何有选择性地展示他们的结果。
以统计方法为中心,实验结果的检验被称为零假设显著性检验,这个过程会产生一个p值。P值只是对事情有一个模糊的描述。“当我们进行实验时,我们想知道的是——我们的假设是真的吗?”本杰明说,“但是,显著性检验回答了一个令人费解的替代问题,那就是,如果我的假设是错误的,我的数据有多大的概率导致错误的结论?”
当然了,p值也有奏效的时候。一个极端但有用的例子是寻找希格斯玻色子(Higgs boson)。希格斯玻色子是物理学家于20世纪60年代首次在理论上提出的粒子。零假设是希格斯玻色子不存在;对立假设是它必须存在。欧洲核子研究中心的物理学家用大型强子对撞机进行了多次实验,得到了极其小的p值,以至于如果假设不存在希格斯玻色子的话,其结果发生的可能性就只有350万分之一。这么小的p值意味着,没有希格斯玻色子的粒子物理标准模型几乎不可能是正确的。
但是,物理学的这种精确度在其他学科是无法达到的。当做人的心理学实验的时候,p值永远不会达到300万分之一。P值为0.05时,在许多重复实验中,每20次实验中就有1次实验错误地否认了正确的假设。这就是为什么统计学家很早以前就增加了“置信区间”这个概念,作为一种让科学家估计误差或不确定性的方法。置信区间在数学上与p值息息相关。P值在0到1之间变动。如果把1减去0.05,得到的0.95就是95%的首选置信区间。但是,但是,置信区间只是一个比较好地概括实验结果的方法,可以体现多种效应量(effect size,做了实验处理的平均结果与不做实验处理的平均结果之间的差异)。格林兰德说:“置信区间也没有任何东西能激发人们的信心。”随着时间的推移,置信区间和p值一样,给人们提供了一种确定性的错觉。
P值本身不一定是问题的本质所在。期刊编辑、科研资助机构和监管机构宣称,p值的分析在论文中是一个非常有用的工具。因此,令人担忧的情况正在发生,统计显著性的重要性被夸大或过分强调了。2015年,可重复性危机项目(现为开放科学中心)开展了一项实验,对100篇重要的社会心理学论文进行了重复性检验,结果发现只有36.1%的论文的结论可以被重复出来。2018年,社会科学可重复性项目评估了《自然》与《科学》在2010年至2015年间发表的21项社会科学实验研究的可重复性。他们发现,与原研究相比,其中只有13项研究中(约占总研究的62%)的重复实验产生了显著结果。
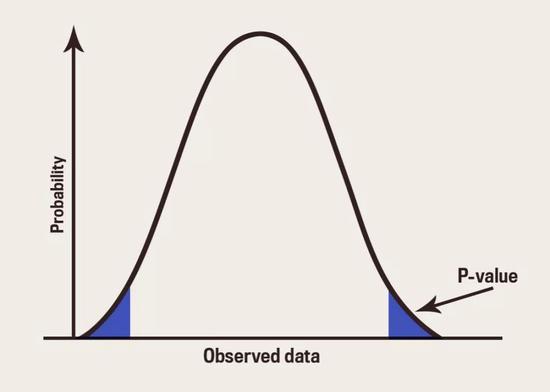
图片来源:slate
从0.05到0.005
很多学科的科学家已经达成了共识:对p值的误解,以及过分强调统计显著性,才是真正的问题,尽管有些人对滥用p值的严重性持较温和的态度。美国康涅狄格大学的社会心理学家布莱尔·约翰逊(Blair T。 Johnson)说:“从长远来看,科学界经常是这样子的,钟摆会在两个极端之间摇摆,你必须接受这一点。”他说,这一轮p值危机的好处是,可以提醒科学家谨慎对待实验结果。
但是,要想真正取得进展,科学家必须就解决方案达成共识,这是很困难的。尽管如此,有用的建议还是很多的。这些建议包括改变统计方法,或者改变统计分析的使用方式等。最突出的观点已经在一系列论文中提出,这些论文始于2016年的美国统计协会声明,其中20多位统计学家就改革的若干原则达成了一致意见。随后,该协会所属的一本期刊还专门制作了特刊,就这一事件发表了一系列文章。
2018年,由72位科学家组成的小组在《自然·人类行为》上发表了一篇名为《重新定义统计意义》的评论文章,赞同将统计显著性的阈值从0.05调整到0.005。这篇文章的主要作者本杰明认为:“这是一个不完美的短期解决方案,但可以立即实施。我担心的是,如果我们不立即做这事,我们将失去变革的动力,而我们最终将花费所有的时间争论理想化的解决方案。”
另一些人则认为,重新定义统计显著性没有好处,因为真正的问题是阈值始终存在。今年3月份,瑞士巴塞尔大学的流行病学家、动物学家瓦伦丁·阿姆莱因(Valentin Amrhein)与美国西北大学的统计学家、市场营销专家布莱克利·麦克沙恩(Blakeley McShane)在《自然》杂志上发表了一篇评论文章,主张放弃统计学显著性的概念。他们建议将p值作为一个连续变量,并将置信区间(confidence intervals)重命名为“相容性区间”(compatibility intervals),以反映它们彰显的实际意义:评估数据的相容性,而不是置信度。
显然,有更好的(至少是更直接的)统计方法可以用。格尔曼经常批评其他人的统计方法,他在工作中根本没有使用零假设显著性检验。他更喜欢贝叶斯方法,这是一种基于初始信念的、更为直接的统计方法,在这种方法中,研究人员接受最初的信念,添加新的证据并更新信念。格林兰德正在推广使用一种叫做稀奇程度(surprisal)的新数学量,可以调整p值以产生信息位(如计算机比特位)。为了检验原假设,0.05的p值仅有4.3比特的信息熵(假设有一枚均匀的硬币,抛硬币出现正面设为0、出现反面设为1,则抛一个硬币事件的信息熵就是1个比特。独立地抛256次硬币的信息熵就是256个比特。那么求解方程0.5x=0.05,解得0.05的概率约为抛掷x=-log20.05=4.3次,于是0.05的p值约为空值的4.3比特的信息熵。
所谓信息熵就是某个概率分布所包含的信息量的多少,这是信息论的基础知识。在信息论中,如果你对一件事情的发生百分之百确定,那么这件事情对你来说的信息熵等于0比特。反过来说,如果你对一件事情是不确定的,那么这件事情对你来说是包含信息熵的。格林兰德认为,如果研究人员不得不在每一个p值旁边加上一个稀奇程度,那么他们将被置于更高的标准之下。强调效应量(effect size),即发现差异的大小,也将有所帮助。

图片来源:pixabay
拥抱不确定性
统计显著性满足了研究人员对确定性的需求。格尔曼说:“这里的原罪是研究人员在得不到确定性的时候却想要确定性。” 或许,现在是时候让我们接受不确定性了。
科学界正在发生微小的变化。《新英格兰医学杂志》的发言人詹妮弗·蔡斯(Jennifer Zeis)说:“我们同意,p值有时被过度使用或被曲解了。对于治疗来说,如果我们认定p<0.05,治疗的结果是有效的;如果p>0.05,治疗是无效的。那么这就是医学的简化主义,它并不总能反映客观事实。”蔡斯同时强调,《新英格兰医学杂志》的研究报告现在已经很少使用p值了,更多是采用置信区间而不是使用p值这个概念。
根据美国食品及药品管理局(FDA)的生物统计学部门的负责人约翰·斯科特(John Scott)的说法,关于p值的应用,临床试验的要求还没有发生任何变化。
麦克沙恩说:“最关键的是,p值不应成为看门人。我们应该采取更全面、更细化和更容易评价的指标。”其实,这个观点在历史上就有人赞同,甚至在与菲舍尔同时代的人中,也有人支持这一观点。比如在1928年,另外两位统计学大师杰尔兹·内曼(Jerzy Neyman)和艾根·佩尔松(Egon Pearson)在撰写统计分析报告时写到:“统计检验本身并没有给出最终的结论,而只是作为一个参考工具帮助人们做出最终的决策。”
撰文:莉迪娅 · 登沃斯(Lydia Denworth)
翻译:张慧铭
参考链接:
Evaluating the Replicability of Social Science Experiments in Nature and Science between 2010 and 2015。 Colin F。 Camerer et al。 in Nature Human Behaviour, Vol。 2, pages 637–644; September 2018。
Moving to a World beyond “p< 0.05。” Ronald L。 Wasserstein, Allen L。 Schirm and Nicole A。 Lazar in American Statistician, Vol。 73, Supplement 1, pages 1–19; 2019。



